KUNCI JAWABAN Matematika kelas 9 halaman 34 35 36 Latihan 8.1 bab 8 Bidang Kartesius

Descartes dikenal sebagai Renatus Cartesius dalam literatur berbahasa Latin, merupakan seorang filsuf dan matematikawan Perancis. Ia mempersembahkan sumbangan yang paling penting yaitu penemuannya tentang geometri analitis, yang akhirnya telah terkenal sebagai pencipta “Sistem koordinat Kartesius”, yang memengaruhi perkembangan kalkulus moderndan menyediakan jalan buat Newton menemukan Kalkulus. Ia memberikan kontribusi yang besar dalam kemajuan di bidang matematika, sehingga dia dipanggil sebagai “Bapak Matematika Modern”.

Descartes, adalah salah satu pemikir paling penting dan berpengaruh dalam sejarah barat modern. Metodenya ialah dengan meragukan

 

semua pengetahuan yang ada, yang kemudian mengantarkannya pada kesimpulan bahwa pengetahuan yang ia kategorikan ke dalam tiga bagian dapat diragukan, yaitu yang berasal dari pengalaman inderawi dapat diragukan, fakta umum tentang dunia semisal api itu panas dan benda yang berat akan jatuh juga dapat diragukan, dan prinsip-prinsip logika dan matematika juga ia ragukan. Dari keraguan tersebut, Descrates hendak mencari pengetahuan apa yang tidak dapat diragukan yang akhirnya mengantarkan pada premisnya Cogito Ergo Sum yang artinya “aku berpikir maka aku ada”.

Sumber: www.edulens.org

Hikmah yang bisa diambil

1. Keyakinan yang sempurna dan mutlak terhadap keberadaan adanya Tuhan, dan semua obyek di dunia ini adalah ciptaan Tuhan.

2. Tidak mudah puas terhadap sesuatu yang sudah didapatkan, sehingga terus berfikir melakukan inovasi untuk menemukan sesuatu yang baru.

3. Manusia diciptakan oleh Tuhan dengan bentuk yang sempurna, oleh karena itu manusia harus menggunakan akal dan pikirannya untuk memanfaatkan lingkungan dengan sebaik-baiknya.

4. Saling membantu dan kerja sama sesama manusia agar terjadi interaksi yang positif dalam melakukan aktifitas dan belajar

1. Tiga dari Empat titik yang dinyatakan dalam koordinat berikut memiliki sifat yang sama.                     Tentukan titik yang memiliki sifat yang berbeda dengan yang lainnya dan berikan alasanmu!

i.    (-2, 1), (-4, 5), (2, -3) dan (-1, 3) iii. (1, -3), (2, -7), (5, 6) dan (4, -4)

ii. (1, 2), (-2, 4), (3, 6) dan (5, 7) iv. (-3, -6), (-4, -7), (-5, -8) dan (-1, 1)

Penyelesaian:

i. (2,-3), tiga titik lainnya berada pada kuadran II

ii. (-2,4), tiga titik lainnya terletak pada kuadran I

iii. (5,6), tiga titik lainnya terletak pada kuadran IV

iv. (-1,1), tiga titik lainnya terletak pada kuadran III

2. Gambarkan dan hubungkan titik-titik di bawah ini untuk membentuk suatu bangun.

1(7, 1) 2(4, - 2) 3(4, - 1) 4(2, - 1) 5(- 1, - 1)6(- 1, 1) 7(- 1, 3) 8(2, 3) 9(4, 3) 10(4, 4)

3. Tulis koordinat yang berhubungan terhadap titik di bawah ini

i. titik A vi.    titik B

ii. titik C vii.   titik D

iii. titik E viii. titik F

iv. titik G ix.    titik H

v. titik I x. titik J

Penyelesaian:

i.    (-4, 4) vi. (3, 4)

ii. (-4, -2) vii. (5, -3)

iii. (8, 6)         viii. (-6, 2)

iv. (9, -2)        ix. (-7, -3)

v.   (6, 2)     x. (2, -2)

4. Gambarkan segi banyak dengan titik sudut yang diberikan.

5. Deskripsikan kesalahan dari solusi berikut

        i. Menggambarkan (7, 6) pada bidang kartesius, mulai dari (0, 0) dan bergerak 7 satuan                     kekanan dan 6 satuan keatas.

        ii. Menggambarkan (-7, -5) pada bidang kartesius, mulai dari (0, 0) dan bergerak 7  `                        satuan kekanan dan 5 satuan kebawah.

Penyelesaian:

i. Tidak ada yang error
ii. Yang benar adalah mulai dari (0, 0) dan bergerak 7 satuan kekiri dan 5 satuan kebawah.

        6. Gambarkan titik dan tentukan jarak antara dua titik. 

i.    (2, -4), (8, -4) iv. (-8, -3), (6, -3)

ii. (5, 4), (5, -1) v. (-5, 4), (7, 4)

iii. (-2, 1), (-2, 9) vi. (-3, -3), (-3, 5)

Penyelesaian:

i. Karena ordinatnya adalah sama, maka jaraknya adalah selisih absisnya yaitu8 – 2 = 6.
ii. Karena absisnya adalah sama, maka jaraknya adalah selisih ordinatnya yaitu 4 – (-1) = 5
iii. K arena absisnya adalah sama, maka jaraknya adalah selisih ordinatnya yaitu 9 – 1 = 8.
iv. Karena ordinatnya adalah sama, maka jaraknya adalah selisih absisnya yaitu 6 – (-8) = 14.
v. Karena ordinatnya adalah sama, maka jaraknya adalah selisih absisnya yaitu 7 – (-5) = 12.
vi. Karena absisnya adalah sama, maka jaraknya adalah selisih ordinatnya yaitu 5 – (-3) = 8.

`       7. Tentukan bentuk segiempat ABCD dengan titik koordinatnya i. A(0, 5), B(0, 1), C(6, 1) dan                 D(6, 5)

            ii. A(0, 5), B(-2, 1), C(0, -3) dan D(2, 1)

Penyelesaian:

i. Persegi panjang

ii. Belah ketupat

8. Dalam menentukan arah sering juga digunakan arah jarum jam; yaitu, sebagai acuannya adalah arah di hadapan objek yang didefinisikan sebagai arah jam 12. Dengan demikian sebelah kanan objek sebagai arah jam 3 dan sebelah objek arah jam 9. Misalkan ada 3 orang I, II, III yang menghadap ke arah utara. Kemudian posisi dari II adalah 10 m dari I dengan arah jam 01.30 dan posisi dari III adalah 8 m dari II dengan arah jam 10.30. Gambarkan posisi dari I, II, III pada bidang kartesius. Kemudian berilah petunjuk kepada 3 orang tersebut supaya bisa berkumpul pada orang ketiga jika 3 orang tersebut hanya bisa bergerak ke depan, ke belakang, ke kiri dan ke kanan.

 Penyelesaian:
Buatlah bidang koordinat dengan arah utara selatan sebagai Sumbu-Y dan arah timur barat sebagai Sumbu-X. Dimisalkan orang I berada pada koordinat (0,0). Kemudian karena orang II berada pada arah jam 01.30 dan sejauh 10 meter dari orang I maka orang II terletak pada 5 ke utara dan 5  ^ 2 ke timur dari orang I. Dengan demikian letak koordinat dari orang II adalah (5 ^2 , 5 ^2 ). Sedangkan orang III berada pada arah jam 10.30 dan sejauh 8 meter dari orang II maka orang III terletak pada 4 ke utara dan 4  ^ 2 ke barat dari orang II. Dengan demikian letak koordinat dari orang III adalah ( ^2 , 9^2 ). Petunjuk untuk orang I: bergerak ke depan sejauh 9^2 dan ke kenan sejauh   2 .

Petunjuk untuk orang II: bergerak ke depan sejauh 4 ^2Petunjuk untuk orang III: Diam di tempat. dan ke kekiri sejauh 4^ 2 .

9. Seorang anak pada pagi hari dari rumah pergi ke sekolahnya dengan bersepeda. Untuk mencapai sekolahnya dia harus bergerak ke arah tenggara sejauh 4 km kemudian ke arah timur sejauh 2 km. Pada saat pulang sekolah anak tersebut pergi ke toko buku. Untuk kesana anak tersebut harus menuju ke arah barat daya sejauh 1 km dan ke arah barat sejauh 0.5 km. Gambarlah letak dari rumah, sekolah dan toko buku pada bidang kartesius. Kemudian bagaimana caranya anak tersebut supaya tiba lagi dirumah?

Penyelesaian:

Buatlah bidang koordinat dengan arah utara selatan sebagai Sumbu-Y dan arah timur barat sebagai Sumbu-X. Dimisalkan rumah berada pada koordinat (0,0). Kemudian karena sekolah berada pada arah tenggara sejauh 4 km kemudian

kearah timur sejauh 2 km dari rumah maka sekolah terletak pada 2√ 2  ke timur dari rumah. Dengan demikian letak koordinat dari sekolah

adalah (2 + 2 2 , -2√2 ). Sedangkan toko buku berada pada arah barat daya sejauh 1 km dan kearah barat sejauh 0.5 km dari sekolah maka toko buku terletak pada 1/2 √2  ke selatan dan   

1/2 + 1/2 √2  ke barat dari sekolah. Dengan demikian letak koordinat dari toko buku adalah 

Supaya siswa tersebut kembali lagi ke rumah maka haruslah                     berjalan ke selatan sejauh 

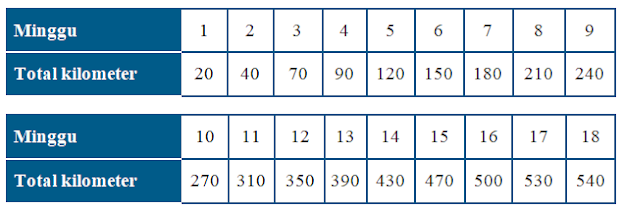
10. Tabel di bawah ini menunjukkan jauhnya lari dalam kilometer pada 18 minggu

untuk program latihan marathon.

a. Tuliskan tabel untuk jarak lari selama setiap minggu latihan.

b. Tampilkan data dari bagian (a) dalam grafik

c. Buatlah tiga pengamatan grafik

d. Jelaskan pola yang ditunjukkan dalam grafik

Penyelesaian:

a. Tabel jarak lari setiap minggu latihan

c. tiga pengamatan dari grafik

- Jarak lari konstan atau tetap pada minggu ke-5 hingga ke-10 dan juga terjadi pada minggu ke-11             hingga ke-15.

- Jarak lari berkurang pada minggu ke-4 dan minggu ke-18.

- Jarak lari terbesar terjadi pada minggu ke-11 hingga ke-15

d. Pola yang ditunjukkan dalam grafik adalah sering terjadinya jarak lari yang konstan dan kadang-            kadang terjadi penurunan dan penambahan jarak lari.

Rangkuman MTK kelas 9 bab 8 bidang kartesius

Kerjakan dengan teman sebangkumu.

a. Siapkan dua lembar kertas berpetak

b. Berilah label pada kertas berpetak pertama dan kedua masing-masing dengan

huruf x dan y

c. Di tengah-tengah kertas berpetak dengan label x, buatlah garis bilangan horizontal seperti yang ditunjukkan pada gambar di bawah ini. Di tengah-tengah kertas berpetak dengan label y, buatlah garis bilangan vertikal.

-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7

d. Potong garis bilangan vertikal dan tempel pada bilangan garis horizontal sehingga nol saling berimpitan dan garis horisontal dan vertikal saling tegak lurus.

a. Berapa banyak daerah yang terbentuk? Beri tanda 1 s/d banyaknya daerah dengan urutannya dari kanan atas kemudian bergerak berlawanan arah jarum jam. (Daerah-daerah ini selanjutnya disebut sebagai kuadran; yaitu kuadran 1, kuadran 2, dst)

b. Gambarkan titik perpotongan antara garis vertikal dan horisontal.

c. Jelaskan letak titik pada bagian (b) terhadap garis horisontal.

d. Jelaskan letak titik pada bagian (b) terhadap garis vertikal.

(Titik pada bagian (b) disebut sebagai titik asal dan dapat ditulis sebagai pasangan bilangan (letak terhadap garis horisontal, letak titik pada garis vertikal)).

 

 

Berdasarkan kegiatan di atas:

Kerjakan dengan teman sebangkumu, gunakan lembaran kerjamu pada Kegiatan 8.2.

Kegiatan 8.2.a. Tempatkan titik pada posisi akhir dari langkah-langkah berikut ini

Langkah 1. Mulailah dari titik asal (0,0) Langkah 2. Bergeraklah 2 satuan ke kanan Langkah 3. Bergeraklah 3 satuan ke atas

Dalam bentuk pasangan bilangan, posisi akhir dari Langkah 1 sampai dengan langkah

3 adalah (2, 3).

Kegiatan 8.2.b. Tempatkan titik pada posisi akhir dari langkah-langkah berikut ini

Langkah 1. Mulailah dari titik asal (0, 0) Langkah 2. Bergeraklah 2 satuan ke kanan Langkah 3. Bergeraklah 3 satuan ke bawah

Dalam bentuk pasangan bilangan, posisi akhir dari Langkah 1 sampai dengan langkah

3 adalah (2, -3).

Kegiatan 8.2.c. Tempatkan titik pada posisi akhir dari langkah-langkah berikut ini

Langkah 1. Mulailah dari titik asal (0, 0) Langkah 2. Bergeraklah 2 satuan ke kiri Langkah 3. Bergeraklah 3 satuan ke atas

Dalam bentuk pasangan bilangan, posisi akhir dari Langkah 1 sampai dengan langkah

3 adalah (-2, 3).

 

Kegiatan 8.2.d. Tempatkan titik pada posisi akhir dari langkah-langkah berikut ini

Langkah 1. Mulailah dari titik asal (0, 0) Langkah 2. Bergeraklah 2 satuan ke kiri Langkah 3. Bergeraklah 3 satuan ke bawah

Dalam bentuk pasangan bilangan, posisi akhir dari Langkah 1 sampai dengan langkah

3 adalah (-2, -3).

Berdasarkan kegiatan di atas:

 

Kerjakan dengan teman sebangkumu. Gunakan lembaran kerjamu pada Kegiatan 8.3.

Tempatkan titik-titik pada bidang koordinat berikut (1, 2), (-1, -2) , (1, -2), dan    (-1, 2) pada bidang kartesius. Terletak pada kuadran berapakah titik-titik tersebut? Bagaimana tanda (positif atau negatif) absis dan ordinat titik-titik tersebut? Jika kamu meletakkan titik lain yang terletak pada kuadran yang sama dengan titik-titik tersebut, apakah tandanya akan sama dengan titik tersebut? Jelaskan dan simpulkan mengenai sifat dari absis dan ordinat pada kuadran tersebut.

 

Kerjakan dengan teman sebangkumu, gambar dan hubungkan titik untuk membuat

bangun. Deskripsikan dan warnai gambar ketika kamu mendapatkannya.

1(10, 11) 2(8, 13) 3(6, 14) 4(4, 13) 5(2, 11)

6(-2, 4) 7(-5, 3) 8(-7, -1) 9(-3, 2) 10(-1, 1)

11(-1, -3) 12(0, -6) 13(-2, -8) 14(1, -7) 15(1, -8)

16(0, -9) 17(0, -10) 18(1, -9) 19(2, -10) 20(2, -9)

21(3, -10) 22(3, -9) 23(2, -8) 24(2, -7) 25(5, -7)

26(6, -6) 27(6, -8) 28(5, -9) 29(5, -10) 30(6, -9)

31(7, -10) 32(7, -9) 33(8, -10) 34(8, -9) 35(7, -8)

36(7, -6) 37(8, -4) 38(10, 2) 39(13, -1) 40(13, 1)

41(12, 3) 42(9, 5) 43(7, 6) 44(7, 9) 45(8, 10)

Sumber: Dokumen Kemendikbud

Gambar 8.1 Deskripsi titik koordinat

1. Bagaimana kamu menggambarkan lokasi suatu titik pada bidang kartesius?

2. Kerjakan secara mandiri. Gambarlah “titik ke titik” dengan menggunakan paling

sedikit 20 titik untuk menggambarkan benda yang kamu sukai.

 

 

Buatlah pertanyaan yang memuat kata “kartesius” dan “kuadran”.

Langkah menggambarkan pasangan bilangan (a, b) ke bidang koordinat Langkah 1. Mulailah dari titik asal (0, 0)

Langkah 2. Jika a > 0 maka gerakkan |a| satuan kekanan dan jika a < 0 maka

gerakkan |a| satuan kekiri

Langkah 3. Jika b > 0 maka gerakkan |b| satuan keatas dan jika b < 0 maka gerakkan

|b| satuan kekiri

Langkah 4. Titik akhir dari Langkah 1 sampai dengan Langkah 3 merupakan posisi

titik koordinat

 

 

Pasangan bilangan yang mana yang berhubungan dengan titik C?

A(4,5) B(-4,5) C(4,-5) D(-4,-5)

Y

 

  6

              D                            5

                   4

                   3

                   2

                   1

 

                                                      F 

  

  

  

  

 

                                           0               u       X

 

-8   -7   -6   -5   -4   -3  -2  -1 0 1 2 3 4 5 6 7

 

8 9 10

 

                  -1

                  -2

  -3

                  -4

              E 5

                  -6

 

  

  

  

                        C 

  

 

Gambar 8.2 Gambar titik koordinat

Alternatif Penyelesaian:

Diketahui : Gambar titik koordinat 8.2 Ditanya : Posisi titik C

Jawab :

Titik C adalah 4 satuan ke kanan dari titik asal dan 5 satuan kebawah. Jadi koordinat-x adalah 4 dan koordinat-y adalah -5. Jadi pasangan bilangan (4, -5) berhubungan dengan titik C. Dengan demikian jawaban yang benar adalah C.

 

 

Gambarkan titik (a) (-1, 2) dan (b) (0, –4 1 ) pada bidang kartesius. Deskripsikan

letak dari setiap titik. 2

Alternatif Penyelesaian:

Diketahui : titik (a) (-1, 2) dan (b) (0, –4 1 )

2

Ditanya : Deskripsikan letak setiap titik

Jawab :

a. Langkah 1. Mulai dengan titik asal. Langkah 2. Gerakkan 1 satuan ke kiri Langkah 3. Gerakkan 2 satuan keatas.

b. Lalu gambar titiknya. Jadi titik berada pada kuadran II.

Langkah 1. Mulai dengan titik asal.

Langkah 2. Gerakkan 0 satuan ke kanan

 

Langkah 3. Gerakkan

 

4 1 satuan kebawah

2

 

Lalu gambar titiknya. Jadi titiknya pada sumbu-Y.

Tabel di bawah ini menunjukkan perubahan kedalaman suatu sungai tiap jam, mulai dari tengah malam hingga jam 8 pagi.

Jam, x 0 1 2 3 4 5 6 7 8

Kedalaman dikurangi 0

100 cm, y cm 60

cm 70

cm 50

cm 40

cm 30

cm 20

cm 40

cm 60

cm

a. Gambarlah data di atas dalam suatu grafik

b. Buat tiga pengamatan dari grafik tersebut

 

Alternatif Penyelesaian:

Diket : Tabel di atas

Ditanya :

a. Gambarlah data di atas dalam suatu grafik

b. Buat tiga pengamatan atas grafik tersebut

Jawab :

a. Tulis data di atas menjadi pasangan bilangan yaitu (0,100),(1,160),(2,170),(3,1 50),(4,140), (5,130), (6,120),(7,140) dan (8,160). Gambar dan beri label untuk setiap pasangan bilangan. Kemudian hubungkan pasangan bilangan dengan garis.

Jam Setelah Tengah Malam

Gambar 8.3 Gambar titik koordinat untuk data

b. Berikut tiga kemungkinan pengamatan:

• Kedalaman sungai berkurang dari jam 02.00 malam hingga jam 06.00 pagi

• Kedalaman sungai bertambah dari jam 00.00 sampai dengan jam 02.00 pagi dan jam 06.00 sampai dengan jam 08.00 pagi.

• Pertambahan kedalaman sungai terbesar terjadi pada 00:00 hingga 01:00

pagi.

 

 

1. Berdasarkan contoh 1 didapatkan koordinat titik C. misalkan jawabanmu adalah (a,b). Gambarkan titik-titik (a,-b), (-a,-b) dan (-a,b). Deskripsikan letak titik-titik tersebut! Buatlah garis yang menghubungkan titik-titik tersebut! Di koordinat manakah garis-garis tersebut memotong sumbu-X dan sumbu-Y?

2. Tabel di bawah ini menunjukkan perubahan suhu tiap jam mulai dari tengah hari hingga jam 6 malam.

Jam setelah tengah malam, x 0 1 2 3 4 5 6

Temperatur, y 40F 60F 50F 10F 00F 00F -60F

a. Gambarlah data di atas pada suatu grafik

b. Buat tiga pengamatan atas grafik tersebut